בצלאל מתווה זווית ישרה

סוד המשולש של המלומד אחמס
בצלאל בן אורי בן חור, המצטיין בחכמה ובדעת בכל מלאכה במתכות ובחרושת אבן ועץ, ערך בפני תלמידיו כמה וכמה הדגמות של סימון זוויות בקשר להקמת בניינים, ביצורים ומחנות.
בהרצאתו הסביר בצלאל שאת רוב ידיעותיו שואב הוא מספר המידות של המלומד המצרי אחמס, שחי לפני חמש מאות שנה בערך. ממנו למד בצלאל שיטה פשוטה ומעניינת להתווית זווית ישרה. וכך עושים את הדבר:
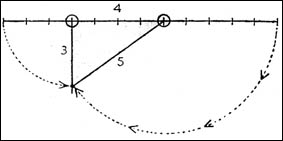
נוטלים חבל של י"ב אמות. קטע של ד' אמות מתוך חבל זה – את הקטע שבין אמה ג' ואמה ח' –מצמידים בשני יתדות לארץ. משני קצות הקטע המתוח המוצמד בצורה כזאת נשארים שני קטעי החבל החופשיים: אורכו של האחד ג' אמות ואורכו של השני ד' אמות. שני אנשים נוטלים את קצותיהם החופשיים, מותחים אותם והולכים זה לקראת זה עד שיפגשו. המקום שבו יפגשו הוא קדקוד של משולש, שזווית אחת שלו – זו שבין הצלע של ג' אמות לבין הצלע של ד' אמות – היא זווית ישרה.
בצלאל רואה בשיטה זו את אחת החכמות הגדולות ביותר בתורת המידות וקורא לה בשם "סוד המשולש ישר-הזווית". והנה עוד סוד, שבצלאל ציין אותו: משולש זה שקיבלנו, אורך צלעותיו ג', ד', ה' אמות כל אחת. תכפיל ג' בג', תוסיף לכך כפל ד' בד', ותקבל... כפל ה' בה'.
ואמנם ג' כפול ג' שווה ט'. ד' כפול ד' שווה ט"ז. ביחד: כ"ה. וה' כפול ה' שווה גם כן לכ"ה.